HILBERT (ESPACE DE)

HILBERT (ESPACE DE)

La théorie des espaces hilbertiens trouve son origine dans celle des développements de fonctions arbitraires en séries de fonctions orthogonales, lesquelles apparaissent le plus souvent comme fonctions propres de certains opérateurs différentiels linéaires (séries de Fourier, fonctions sphériques, théorie des oscillations de Sturm-Liouville). À l’occasion de l’étude des équations intégrales, ébauchées par V. Volterra, I. Fredholm et E. Schmidt, Hilbert définit l’espace l ² des suites de carré sommable, et résout les principaux problèmes posés en interprétant les équations en termes d’endomorphismes de l’espace l ². E. Schmidt, M. Fréchet et F. Riesz donnent ensuite une forme plus géométrique à la théorie de Hilbert, en introduisant le langage des normes, de l’orthogonalité et des bases hilbertiennes, et découvrent que de nombreux espaces fonctionnels classiques sont isomorphes à l ², ou à des sous-espaces vectoriels de cet espace. Dès lors s’impose une présentation axiomatique des espaces préhilbertiens et hilbertiens; elle est essentiellement due à J. von Neumann et à F. Riesz ; le lecteur la trouvera esquissée ci-dessous. Enfin, ces derniers approfondissent considérablement l’étude des endomorphismes des espaces hilbertiens, et créent ainsi un des outils les plus puissants de l’analyse fonctionnelle et de la physique mathématique.

Nous supposons connus les notions fondamentales de l’algèbre linéaire (cf. algèbre LINÉAIRE ET MULTILINÉAIRE), le langage des normes et semi-normes, et la notion de famille sommable ^{[cf. SÉRIES ET PRODUITS INFINIS]}.

Généralités

Espaces préhilbertiens

On appelle espace vectoriel préhilbertien (complexe) un espace vectoriel sur le corps C des nombres complexes, muni d’une forme sesquilinéaire auto-adjointe dont la forme hermitienne associée est positive, c’est-à-dire d’une application de E 憐 E dans C, notée (x , y ) 料 (x |y ), satisfaisant aux conditions suivantes:

– pour tout élément y de E, l’application x 料 (x |y ) est linéaire;

– pour tout couple (x , y ) d’éléments de E, (y |x ) = (x |y );

– pour tout élément x de E, (x |x ) 閭 0.

Le scalaire (x |y ) s’appelle produit hermitien des vecteurs x et y .

On dit que l’espace vectoriel E est préhilbertien séparé, ou hermitien , si la forme, hermitienne considérée est définie positive, c’est-à-dire si la relation (x | x ) = 0 implique la relation x = 0.

Théorème 1. Pour tout couple (x , y ) d’éléments d’un espace préhilbertien E:

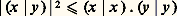(inégalité de Schwarz).

Écartons le cas où l’un des deux vecteurs x et y est nul. Écrivons que, pour tout nombre réel 見 et pour tout nombre complexe 廓 de module 1, le nombre réel:

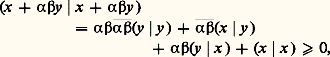ou encore:

par suite, le discriminant de ce trinôme du second degré en 見 est négatif ou nul pour tout nombre complexe 廓 de module 1,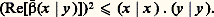

L’inégalité cherchée étant évidente lorsque (x |y ) = 0, écartons ce cas. Nous obtenons alors l’inégalité de Schwarz en posant:

Lorsque l’espace vectoriel E est hermitien, on montre qu’il y a égalité dans l’inégalité de Schwarz si et seulement si les vecteurs x et y sont colinéaires.

Théorème 2. Soit E un espace vectoriel préhilbertien. L’application qui à tout vecteur x de E associe le nombre réel positif 瑩x 瑩 = (x |x )^1/2 est une semi-norme sur E, dite associée à la forme sesquilinéaire (x , y ) 料 (x |y ).

En effet, pout tout nombre complexe 見, 瑩 見x 瑩 = | 見| . 瑩x 瑩. Pour tout couple (x , y ) de vecteurs de E: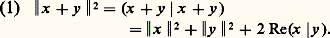

D’autre part:

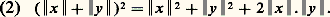L’inégalité triangulaire:

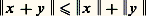découle des relations (1) et (2), de la relation Re(x |y ) 諒 |(x |y )| et de l’inégalité de Schwarz.

La semi-norme précédente est une norme si et seulement si l’espace vectoriel E est hermitien. Le nombre réel positif 瑩x 瑩 s’appelle alors norme hermitienne du vecteur x , et le nombre 瑩x 漣 y 瑩 distance hermitienne des points x et y . Un vecteur de norme 1 est dit unitaire. Dans ces conditions, il y a égalité dans l’inégalité triangulaire si et seulement si les vecteurs x et y sont colinéaires et de même sens, c’est-à-dire s’il existe un couple ( 見, 廓) de nombre réels positifs non tous deux nuls tel que 見x = 廓y .

Espaces hilbertiens

En algèbre, on utilise surtout les espaces hermitiens de dimension finie. En analyse, ce sont les espaces hermitiens de dimension infinie qui interviennent dans la plupart des questions; on est amené à supposer que ces espaces sont complets, c’est-à-dire que toute suite de Cauchy est convergente. Un espace hermitien complet est dit hilbertien. Tout espace hermitien de dimension finie est hilbertien.

Voici deux exemples fondamentaux:

Soit I un ensemble non vide. L’espace vectoriel C^(I) des applications de I dans C nulles sauf pour un nombre fini de valeurs de la variable, muni de la forme ses-quilinéaire qui, aux vecteurs x = ( 﨡ⁱ ) et y = ( 兀ⁱ ), i 捻 I, associe le nombre complexe:

est hermitien; il est hilbertien si et seulement si l’ensemble I est fini.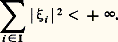

Soit l ²(I) l’espace vectoriel des familles x = ( 﨡ⁱ ), i 捻 I, de nombres complexes telles que:

Si x = ( 﨡ⁱ ) et y = ( 兀ⁱ ), i 捻 I, sont deux éléments de cet espace, la famille ( 﨡ⁱ 兀ⁱ 漣), i 捻 I, est sommable. Muni de l’application:

l ²(I) est un espace hilbertien.

Voici deux autres exemples, dont l’importance est capitale en analyse fonctionnelle. Soit I un intervalle de R non réduit à un point, et p une fonction à valeurs réelles continue sur I, prenant des valeurs strictement positives en tout point intérieur à I. Soit 暈(I, p ) l’espace vectoriel des fonctions f continues sur I à valeurs complexes telles que: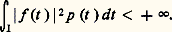

Pour tout couple (f , g ) d’éléments de cet espace vectoriel, fgp est intégrable sur I. Muni de l’application:

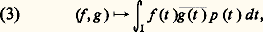暈(I, p ) est un espace vectoriel hermitien, mais ce n’est pas un espace hilbertien. En revanche, l’espace vectoriel L²(I, p ) des classes de fonctions f à valeurs complexes, mesurables sur I et telles que:

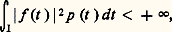muni de l’application définie par la formule (3), est hilbertien, ce qui met en évidence l’intérêt de la théorie de Lebesgue pour toutes ces questions.

Orthogonalité

On dit que deux vecteurs x et y d’un espace hermitien E sont orthogonaux si leur produit hermitien est nul: (x |y ) = 0. Puisque (y |x ) = (x |y ), cette relation est symétrique.

On dit que deux parties A et B de E sont orthogonales si, pour tout élément x de A et pour tout élément y de B, (x |y ) = 0. L’ensemble, noté A size=1^旅, des vecteurs orthogonaux à une partie A de E est un sous-espace vectoriel fermé de E, appelé orthogonal de A. L’orthogonal de E est réduit au vecteur nul.

Soit F un sous-espace vectoriel de E. On dit que F admet un supplémentaire orthogonal s’il existe un sous-espace vectoriel G de E orthogonal à F tel que E = F 簾 G. Alors G = F size=1^旅; c’est pourquoi F size=1^旅 s’appelle le supplémentaire orthogonal de F dans E. La projection d’un vecteur x de E sur F parallèlement à G s’appelle projection orthogonale de x sur F. Sous ces mêmes hypothèses, (F size=1^旅) size=1^旅 = F. En effet, il est évident que (F size=1^旅) size=1^旅 contient F. Soit donc x un élément de (F size=1^旅) size=1^旅; écrivons x sous la forme x = y + z , où y 捻 F size=1^旅 et z 捻 F. Il s’ensuit que:

c’est-à-dire que (y |y ) = 0. Ainsi, y = 0, et x = z . Le vecteur x appartient donc à F.

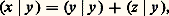Soit maintenant (Fⁱ ), i 捻 I, une famille de sous-espaces vectoriels de E orthogonaux deux à deux, et F leur somme. Alors cette somme est directe; c’est pourquoi l’on dit que F est somme directe orthogonale des sous-espaces vectoriels Fⁱ .

Soit S = (x ⁱ ), i 捻 I, une famille de vecteurs d’un espace hermitien E. On dit que S est orthogonale si, pour tout couple (i , j ) d’éléments distincts de I, les vecteurs x ⁱ et x ^j sont orthogonaux. Dans ces conditions, pour toute partie finie J de I:

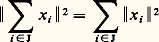(théorème de Pythagore). On dit que S est orthonormale si, de plus, pour tout élément i de I, le vecteur x ⁱ est unitaire; la somme des droites Cx ⁱ est alors directe orthogonale.

On dit enfin que S est une base hilbertienne de E si S est orthonormale, et si le sous-espace vectoriel engendré par S est dense dans E. Cette notion est mieux adaptée à l’analyse que celle de base orthonormale.

Par exemple, la base canonique (e ⁱ ), i 捻 I, de l’espace vectoriel C^(I) est orthonormale; cette famille est une base hilbertienne, dite canonique, de l’espace hilbertien l ²(I), car C^(I) est dense dans l ²(I).

Voici un autre exemple, lié de manière essentielle à la théorie des séries de Fourier. Soit 暈(T) l’espace vectoriel des fonctions continues sur R à valeurs complexes et admettant l pour période, muni du produit hermitien: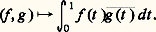

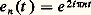La famille (e ⁿ ), n 捻 Z, des fonctions définies par les formules:

est une base hilbertienne de 暈(T); les éléments du sous-espace vectoriel engendré par S s’appellent polynômes trigonométriques. L’espace hermitien 暈(T) n’est pas complet; il peut s’identifier à un sous-espace vectoriel de l’espace vectoriel hilbertien L²([0, 1]), dense dans L²([0, 1]). La famille (e ⁿ ), n 捻 Z, apparaît alors comme une base hilbertienne de L²([0, 1]).

Théorie élémentaire

L’étude des espaces hermitiens de dimension finie repose sur le théorème qui suit.

Théorème 3. Tout espace hermitien de dimension finie admet au moins une base orthonormale.

La démonstration s’effectue par récurrence sur la dimension de l’espace hermitien E. Soit donc E un espace hermitien de dimension strictement positive n . Choisissons un vecteur unitaire e ¹. L’ensemble H des vecteurs orthogonaux à e ¹ est un hyperplan de E, car c’est le noyau de la forme linéaire non nulle x 料 (x |e ¹). De plus, e ¹ n’appartient pas à H, si bien que E est somme directe orthogonale de la droite Ce ¹ et de H. Il suffit alors d’appliquer l’hypothèse de récurrence à H, qui est de dimension n 漣 1, pour obtenir une base orthonormale de E.

Théorème 4. Soit E un espace hermitien et F un sous-espace vectoriel de E de dimension finie.

– Pour tout vecteur x de E, il existe un couple (y , z ) et un seul de vecteur de E tel que y 捻 F size=1^旅, z 捻 F et x = y + z . Autrement dit, le sous-espace vectoriel F size=1^旅 est supplémentaire orthogonal de F dans E. Par suite, (F size=1^旅) size=1^旅 = F. Enfin, pour tout vecteur u de F différent de z , 瑩x 漣 u 瑩 礪 瑩x 漣 z 瑩.

– Si F est muni d’une base orthonormale (e ¹, e ², ..., e ^p ), alors:

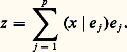Munissons F d’une base orthonormale (e ¹, e ², ..., e ^p ). Le vecteur z , s’il existe, peut s’écrire d’une manière et d’une seule sous la forme z = 見¹e ¹ + ... + 見^p e ^p ; or,

par suite, les vecteurs y et z sont nécessairement définis par les formules:

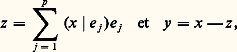ce qui prouve l’unicité du couple (y , z ). Réciproquement, les vecteurs ainsi définis conviennent visiblement.

Soit maintenant u un vecteur de F. Le vecteur x 漣 z est orthogonal à F, et le vecteur z 漣 u appartient à F. Donc:

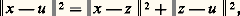ce qui achève la démonstration.

Corollaire 1. Toute famille orthonormale d’éléments d’un espace hermitien E de dimension finie peut être complétée en une base orthonormale de E.

Soit en effet F le sous-espace vectoriel engendré par une famille orthonormale L. D’après le théorème, F size=1^旅 est supplémentaire orthogonal de F dans E. Il existe une base orthonormale L de F size=1^旅. La base de E obtenue en réunissant L et L convient.

Corollaire 2. Soit (e ¹, e ², ..., e ^p ) une famille orthonormale de vecteurs d’un espace hermitien E, et x un vecteur de E. Pour tout élément j de [1, n ], on pose 﨡^j = (x |e ^j ). Alors la fonction f qui à tout élément (¹,², ...,^p ) de C^p associe le nombre réel positif:

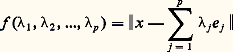admet un minimum strict au point ( 﨡¹, 﨡², ..., 﨡^p ). Autrement dit, pour approcher le mieux possible (en norme) un vecteur x par des éléments de la forme: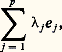

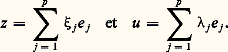il convient de prendre^j = 﨡^j pour tout j 捻 [1, p ]. Posons en effet:

Puisque u appartient au sous-espace vectoriel F engendré par e ¹, e ², ..., e ^p , nous savons que, si u z :

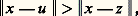ce qu’il fallait prouver.

Soit, par exemple, f une fonction continue à valeurs complexes admettant 1 pour période, et p un entier naturel. Parmi les polynômes trigonométriques de la forme:

celui qui approche le mieux f en moyenne quadratique est le polynôme:

somme partielle à l’ordre p de la série de Fourier de f.

Procédé d’orthonormalisation de Schmidt. Soit E un espace hermitien, (e ¹, e ², ..., e ^p ) une famille orthonormale de vecteurs de E, et F le sous-espace vectoriel de E engendré par cette famille. On suppose que F est différent de E, et on considère un vecteur x de E n’appartenant pas à F. Il existe alors un vecteur e ^{p +1} de E et un seul tel que:

– la famille (e ¹, e ², ..., e ^p , e^{p +1}) soit orthonormale;

– le vecteur e ^{p +1} appartienne au sous-espace vectoriel F 簾 Cx ;

– le scalaire (e ^{p +1} | x ) soit réel positif.

De plus, le vecteur e ^{p +1} est donné par la formule: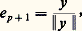

où: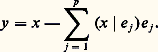

Par récurrence, on en déduit le théorème suivant.

Théorème 5. Soit (x ⁿ ), n 捻 N, une famille libre d’éléments d’un espace hermitien E. Il existe alors une famille orthonormale (e ⁿ ), n 捻 N, et une seule de vecteurs de E telle que, pour tout entier n , e ⁿ appartienne au sous-espace vectoriel engendré par les vecteurs x ⁰, x ¹, ..., x ⁿ , et que (x ⁿ |e ⁿ ) soit réel positif. On dit que (e ⁿ ), n 捻 N, se déduit de (x ⁿ ), n 捻 N, par orthonormalisation. Ces deux familles engendrent le même sous-espace vectoriel F de E.

En particulier, si (x ⁿ ), n 捻 N, est totale, c’est-à-dire si F est dense dans E, (e ⁿ ), n 捻 N, est une base hilbertienne de E. Il en résulte que tout espace hermitien séparable (c’est-à-dire, admettant une famille de vecteurs totale dénombrable) admet une base hilbertienne dénombrable.

Appliquons ces résultats à l’espace hermitien 暈(I, p ) introduit plus haut, en supposant que, pour tout entier naturel n , la fonction x ⁿ : t 料 t ⁿ est un élément de 暈(I, p ). La famille (e ⁿ ), déduite de (x ⁿ ), n 捻 N, par orthonormalisation est constituée de fonctions polynomiales, e ⁿ étant de degré n . La famille (e ⁿ ) s’appelle système de polynômes orthogonaux associé au poids p sur l’intervalle I. Lorsque l’intervalle I est borné, (e ⁿ ), n 捻 N, est une base hilbertienne de 暈(I, p ); il en est de même lorsque I est non borné, s’il existe deux nombres réels strictement positifs 見 et 廓 tels que, pour tout t 捻 I, p (t ) 諒 廓 exp 漣 見|t | (cf. polynômes ORTHOGONAUX).

Étudions enfin les principales propriétés des bases hilbertiennes.

Théorème 6. Soit (e ⁱ ), i 捻 I, une famille orthonormale d’éléments d’un espace hermitien E, F l’adhérence du sous-espace vectoriel engendré par les vecteurs e ⁱ , x un vecteur de E, et ( 﨡ⁱ ), i 捻 I, la famille des composantes de x suivant (e ⁱ ), i 捻 I, c’est-à-dire des scalaires 﨡ⁱ = (x |e ⁱ ).

1. La famille ( 﨡ⁱ ), i 捻 I, est de carré sommable, et:

(inégalité de Bessel).

2. Pour que x appartienne à F, il faut et il suffit que: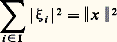

(égalité de Parseval).

Dans ces conditions, la famille ( 﨡ⁱ e ⁱ ), i 捻 I, est sommable, et:

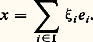3. Pour tout couple (x , y ) d’éléments de F de composantes respectives ( 﨡ⁱ ) et ( 兀ⁱ ), i 捻 I, la famille ( 﨡ⁱ 兀ⁱ 漣), i 捻 I, est sommable, et:

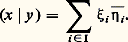Ce théorème est une conséquence immédiate du théorème 4, puisque, pour toute partie finie J de I, la projection orthogonale de x sur le sous-espace vectoriel ^J engendré par la famille (e ⁱ ), i 捻 J, est égale à:

Lorsque (e ⁱ ), i 捻 I, est une base hilbertienne de E, les assertions 2 et 3 s’appliquent à tous les éléments de E.

Corollaire. Soit E un espace hermitien et (e ⁱ ), i 捻 I, une base hilbertienne de E. Alors l’application qui à tout vecteur de E associe la famille de ses composantes dans la base (e ⁱ ) est un isomorphisme de l’espace hermitien E sur un sous-espace vectoriel de l’espace hilbertien l ²(I).

Si l’espace E est hilbertien, cette application est un isomorphisme de E sur l ²(I).

En effet, si E est complet, pour tout élément ( 見ⁱ ), i 捻 I, de l ²(I), la famille ( 見ⁱ e ⁱ ), i 捻 I, est sommable. Alors le vecteur: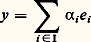

admet 見ⁱ pour i -ième composante.

On peut appliquer ce théorème aux développements en série de fonctions orthogonales (séries de Fourier, polynômes orthogonaux, etc.).

Espaces hilbertiens

Dans la théorie précédente, le théorème de projection orthogonale (théorème 4) a joué un rôle fondamental. Il ne s’étend malheureusement pas au cas d’un sous-espace vectoriel fermé quelconque F d’un espace hermitien. Ainsi, dans l’espace hermitien 暈[ 漣 1, 1]), l’hyperplan fermé noyau de la forme linéaire continue:

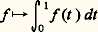n’admet pas de supplémentaire orthogonal. Néanmoins, si F est complet, le théorème 4 s’étend de la manière suivante:

Théorème 7. Soit E un espace hermitien et F un sous-espace vectoriel complet de E. Alors F admet un supplémentaire orthogonal, et (F size=1^旅) size=1^旅 = F.

Ce théorème contient le théorème 4 comme cas particulier, et s’applique aussi au cas où E est hilbertien et F fermé.

La démonstration s’appuie sur le théorème suivant.

Théorème 8. Soit E un espace hermitien, F une partie convexe complète non vide de E, et x un élément de E. Il existe alors un élément z de F et un seul tel que:

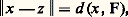où: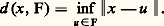

On montre pour cela que toute suite (z ⁿ ) de points de F telle que 瑩x 漣 z ⁿ 瑩 converge vers d (x , F) est une suite de Cauchy. Comme F est complet, la suite (z ⁿ ) admet une limite z dans F, et on vérifie que z convient.

On en déduit facilement le théorème 7, en prouvant que y = x 漣 z est orthogonal à F.

Dégageons quelques conséquences du théorème 7.

Corollaire 1. Soit F un sous-espace vectoriel fermé d’un espace hilbertien E. Si F E, il existe un vecteur non nul de E orthogonal à F.

Corollaire 2. Pour qu’une famille (e ⁱ ), i 捻 I, de vecteurs d’un espace hilbertien E soit totale, il faut et il suffit que le vecteur nul soit le seul vecteur orthogonal à tous les vecteurs e ⁱ .

Corollaire 3. Soit a un vecteur d’un espace hilbertien E. L’application f ^a : x 料 (x |a ) est une forme linéaire dont la norme est égale à celle de a . Autrement dit:

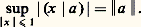Réciproquement, pour toute forme linéaire continue f sur E, il existe un vecteur a de E et un seul tel que f soit égale à l’application x 料 (x |a ). Ainsi, l’application a 料 f ^a est une application semi-linéaire bijective de E sur son dual topologique E.

Corollaire 4. Toute famille orthonormale d’éléments d’un espace hilbertien E peut être complétée en une base hilbertienne de E. En particulier, tout espace hilbertien admet au moins une base hilbertienne (e ⁱ ), i 捻 I. L’application

est alors un isomorphisme de l’espace hilbertien l ²(I) sur E.

On démontre aussi que deux bases hilbertiennes d’un espace hilbertien E sont équipotentes. Le cardinal d’une base hilbertienne de E s’appelle dimension hilbertienne de E.

Encyclopédie Universelle. 2012.